Continuous Time to Sampled Time Transformation

Sampling continuous-time signals

In this chapter, we will cover the sampling theorem and the connection between continuous-time and discrete-time signals. As we have seen in the previous chapter, there is no implicit connection between discrete-time signals and any continuous-time signal. This chapter will establish that connection for a specific class of functions, and explore the conditions for the discrete-time signal to be "representative" of a unique continuous-time signal.

Continuous-time to discrete-time signals

Continuous-time signals are typically defined for all real values. The notation \(x(t)\) implicitly defines a value for \(x(\cdot)\) for every \(t \in \mathbb{R}\). Loosely speaking, the set \(\mathbb{R}\) has "many" elements, and in fact, technically called an uncountable set in mathematical parlance. On the other hand, a discrete-time signal \(x[n]\) is defined only for \(n \in \mathbb{Z}\) (that is, integer values of \(n\)). While it appears that the number of integers is also infinite, is is a countable set, and has "much fewer" elements than \(\mathbb{R}\). For a more detailed treatment of this, I recommend that you take a good course on real analysis, like EE759, when you get the chance.

But, to summarize the key issue here, it appears that the continuous-time signal has much more information in it, and any attempt to convert it to a discrete-time would definitely incur some loss of information. Is this inevitable, or is there some way to go from the continuous-time signal to the discrete-time signal? There is a connection between this property and the frequency content of the continuous-time signal, which we will look at in detail.

The continuous-time Fourier transform

We now quickly revise the continuous-time Fourier transform. Recall that any square-integrable signal \(x(t)\) has a continuous-time Fourier transform \(X(f)\), defined using the analysis equation as

\[\begin{equation} X(f) = \int_{-\infty}^\infty x(t) e^{-j2\pi f t} dt \tag{3.1} \end{equation}\]

and the corresponding synthesis equation allows us to go in the revese direction:

\[\begin{equation} x(t) = \int_{-\infty}^\infty X(f) e^{j2\pi f t} df. \tag{3.2} \end{equation}\]

Typially, textbooks use the \(\Omega = 2\pi f\) notation, but we stick to the \(f\) based notation here for convenience.

An intuitive way to understand the Fourier transform is to consider it as a basis transform from the basis of Dirac impulse signals to that of complex exponentials. That is, if we view the expansion of \(x(t)\) in the basis of impulses, we have

\[\begin{equation} x(t) = \int_{-\infty}^\infty x(\tau) \delta(t - \tau) d\tau. \end{equation}\]

So, Equations (3.1) and (3.2) can be viewed as basis transformations.

In the true sense, the Fourier transform necessarily exists only for square-integrable signals (or absolutely integrable functions), such as \(e^{-t}u(t)\), \(u(t) - u(t - 2)\) etc. However, there are several signals that are not square-integrable for which the continuous-time Fourier transform can be defined, such as \(\delta(t)\), \(\cos(2\pi f_0 t)\) etc. A table of common continuous-time Fourier transforms can be found in (Oppenheim, Willsky, and Nawab 2005), though you can also refer to online sources like the Wikipedia Fourier transform page. It is a good idea to be familiar with the Fourier transform pairs for some common signals, such as the rectangular signal, sinc, exponentials etc., since they appear commonly in the context of DSP as well.

Band-limited signals

One important class of signals is the class of band-limited signals. These signals are characterized by the fact that their Fourier transform is zero outside a range of frequencies; that is, \(x(t)\) is said to be band-limited if there exists a number positive number \(f_0\) such that \(|X(f)| = 0\) for \(|f| > f_0\). We discuss this with some examples here.

The first thing to note is that time-limited signals cannot be band-limited (can you think about why this is the case?). Now, almost every practical signal that we can come up with seems to be time-limited. So, is the concept of band-limited mythical?

The answer is that, when we perform signal processing, we are largely concerned with a suitable representation of related signals within the time-window within which we operate. For instance, if we are processing a speech signal that lasts from \(t = 0\) to \(2\) seconds, whether the signal \(\cos(200\pi t)\) actually existed for \(t < 0\) or would exist for \(t > 2\) is immaterial. So, if we consider only the interval \(t \in [0, 2]\), whether we consider \(\cos(200\pi t)\) or \((\cos(200\pi t)(u(t) - u(t - 2))\) makes no difference. There are better answers to this question, but this is something that you can think about.

Even if you couldn't appreciate the point made in the previous paragraph, just assume that practical signal processing can be performed using band-limited signals even in practical scenarios.

Now, if we consider the universe of band-limited signals, we start with the traditional sinc function, whose Fourier transform is the rect signal.

Figure 3.1: The sinc signal and its Fourier transform

The sinc signal is important, since it provides us with a recipe to make band-limited signals. Since the sinc's Fourier transform, the rect, is band-limited, any band-limited signal's Fourier transform can be described as the outcome of the product of a (potentially) non-band-limited signal with the rect. This is just a restatement of the fact that the sinc signal is the ideal low-pass filter that cuts off all frequencies outside of its band. So, by controlling the scaling of time, we can change the width in the frequency domain. For instance, the signal \(x(t) = \text{sinc}(t/T)\) and its Fourier transform exhibit the behaviour shown in Figure 3.2.

Figure 3.2: \(\text{sinc}(t/T)\) and its corresponding Fourier transform (see web version for animation).

Other examples of band-limited signals include sinusoids, since they have, by definition, a single frequency. For those who have worked with communication systems, the raised cosine and root-raised cosine signals are also commonly encountered band-limited signals. During this course, we will encounter several other band-limited signals that are useful to know about.

Video pending

Sampling continuous-time signals

Sampling refers to the act of recording the value of a continuous-time signal only at certain values of time. In this course, we will look at the case of sampling at equally spaced time intervals. That is, given a continuous-time signal \(x_c(t)\), if the signal is sampled at \(f_s\) samples per second, or once every \(T_s\) seconds, where \(fT_s = 1\), the sampled version would be

\[ x[n] = x_c(nT_s), n = \ldots -3, -2, -1, 0, 1, 2, 3, \ldots \]

The above representation is that of a sequence that stores only the relevant values of the sampled signal. It is, however, instructive to also look at the continuous-time version of the sampled signal, since that is needed for us to capture the full information of the conversion from the continuous-time to the discrete-time signal. Now, one possible way to represent the sampled signal is to define \(x_d(t) = x_c(t)f(t)\), where \(f(t)\) is a signal that is \(1\) when \(t\) is an integer, and \(0\) otherwise. This, however, has problems, primarily since the energy of such a signal is zero, if we define the energy of a signal to be the squared integral of the signal. More details on this can be learnt in EE759.

To handle this issue of "capturing" at least some of the energy of \(x_c(t)\) during sampling, we define sampling as multiplication of \(x_c(t)\) with the so-called impulse train signal, defined as

\[ s(t) = \sum_{n = -\infty}^\infty \delta(t - nT_s). \]

Strictly speaking, the above is not a signal (or mathematical function) in the true sense, since its value at \(t = nT_s\) is not defined. Remember that \(\delta(t)\) is a function that integrates to \(1\), but is not defined for \(t = 0\). Moreover, we will be using its Fourier transform as well, even though the function is not square integrable. These are aspects that you can revise from your signals and systems course material. Here, we will define the continuous-time version of the sampled signal as

\[ x_d(t) = x(t)s(t) = \sum_{n = -\infty}^\infty x(nT_s)\delta(t - nT_s). \] where \(x(nT_s) = x[n]\).

One interesting, but important property of the impulse train is that its continuous-time Fourier transform is also an impulse train. From Figure 3.3, we see the inverse relation between the impulse trains in the time domain and their corresponding Fourier transforms. This comes in handy, since multiplication by the impulse train for sampling in the time domain directly translates to convolution with the impulse train in the frequency domain. Moreover, the density of these impulses in the time and frequency domain are inversely related; that is, if the sampling frequency increases, the impulses in the frequency domain are further apart, as seen in the figure. We will use this observation to describe the Nyquist sampling criterion.

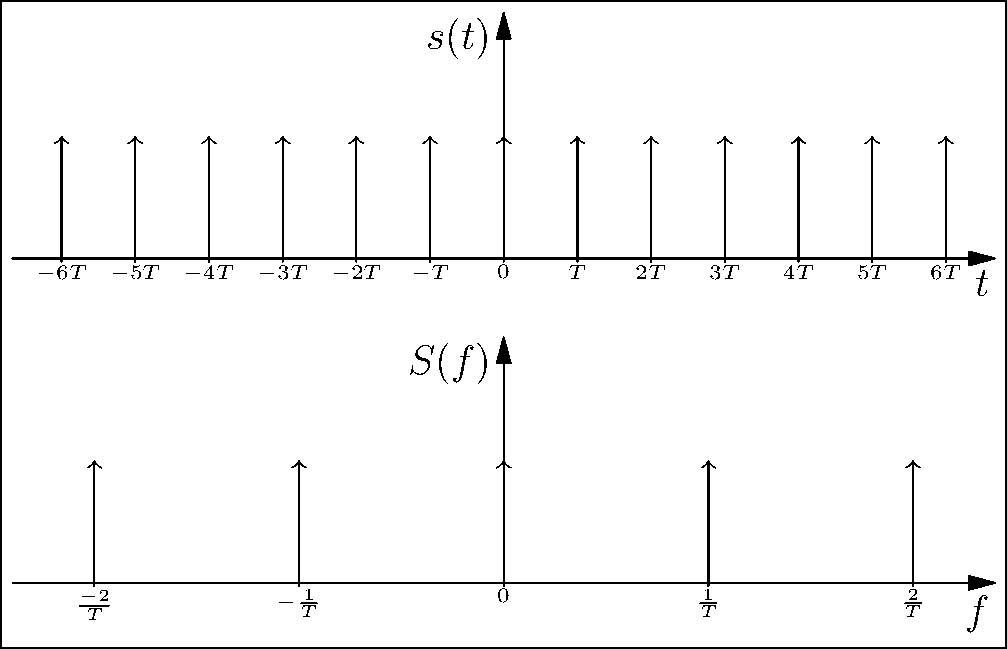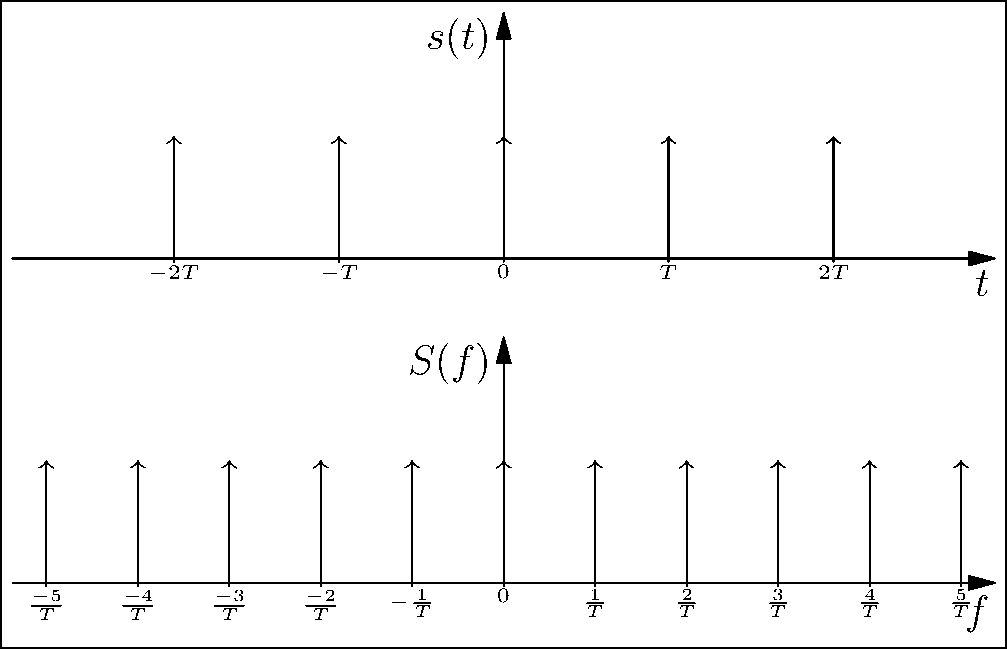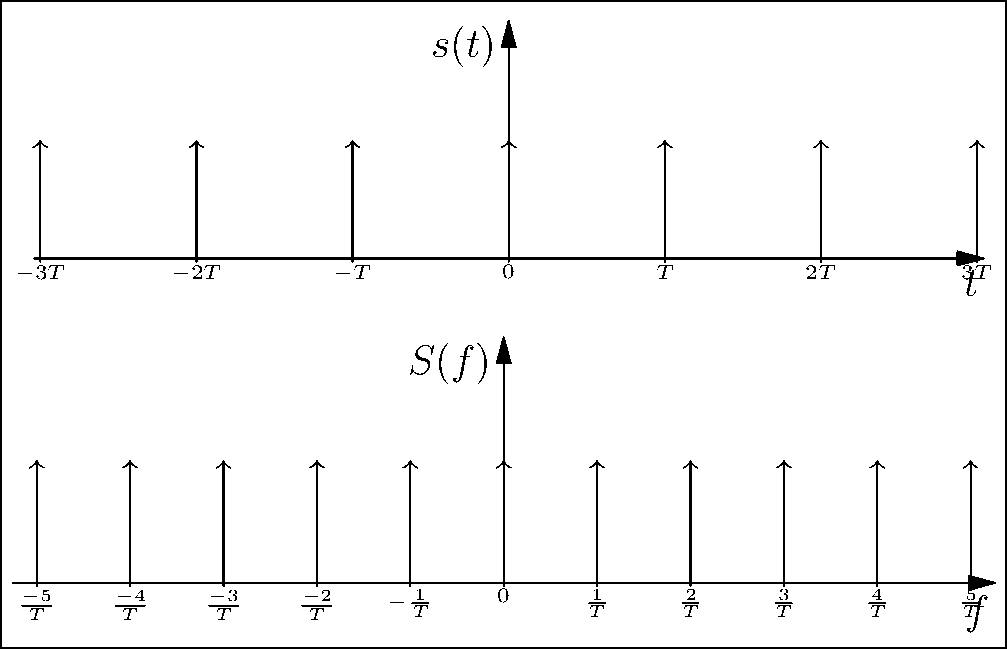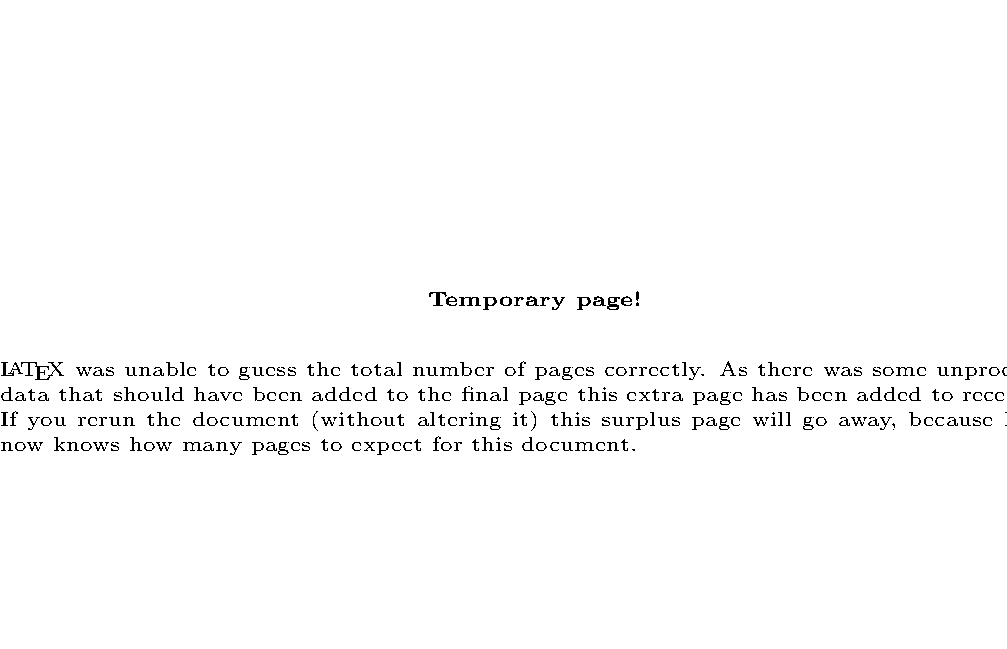
Figure 3.3: Observe that the impulses spread out in the time-domain while they come closer in the frequency domain and vice-versa (see web version for animation).

Can you derive the Fourier transform relationship for the impulse train?

Detour: The wagon wheel effect

If you watch movies or other videos that contain vehicles, you may have observed the wheels of those vehicles. Have you seen that the wheels seem to move incorrectly? This is because of what is known as the wagon wheel effect. This can be understood by viewing the video as a sequence of pictures that have been recorded and are being played back. For instance, if you observe Figure 3.4, you will see that, if the sampling rate (or frame rate) \(f\) of the video is more than twice the true rotation frequency of the wheel, denoted by \(\text{FPS}\), then the rotation of the red dot on the wheel is faithfully reproduced. However, if the rotation is not correctly captured, problems like the one on the right wheel will occur. Even if the sampling is precisely twice the frame rate, the rotation of the dot cannot be disambiguated.

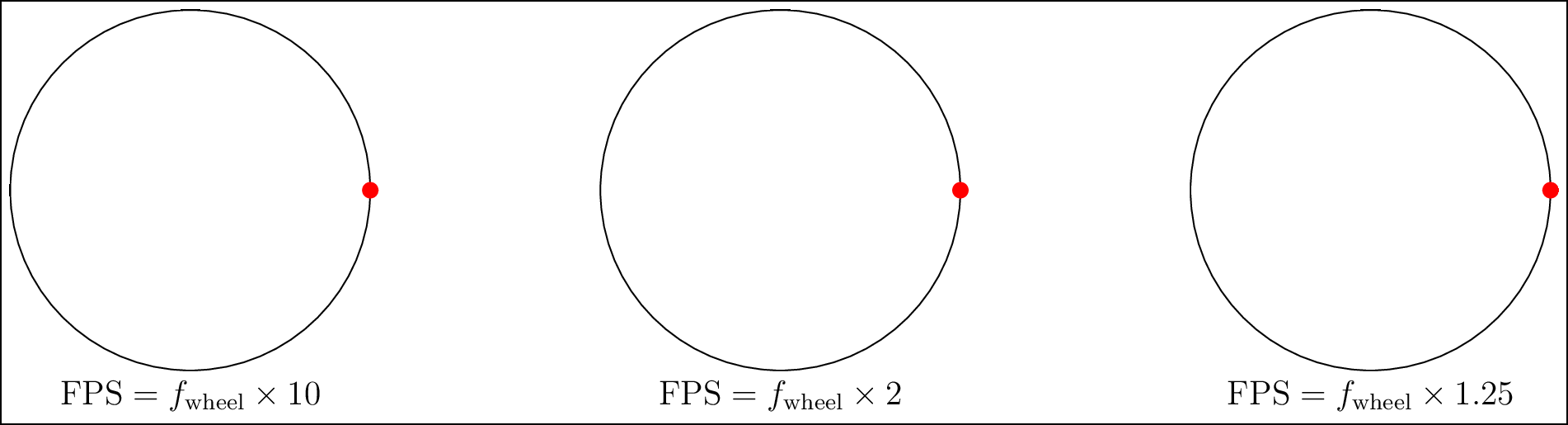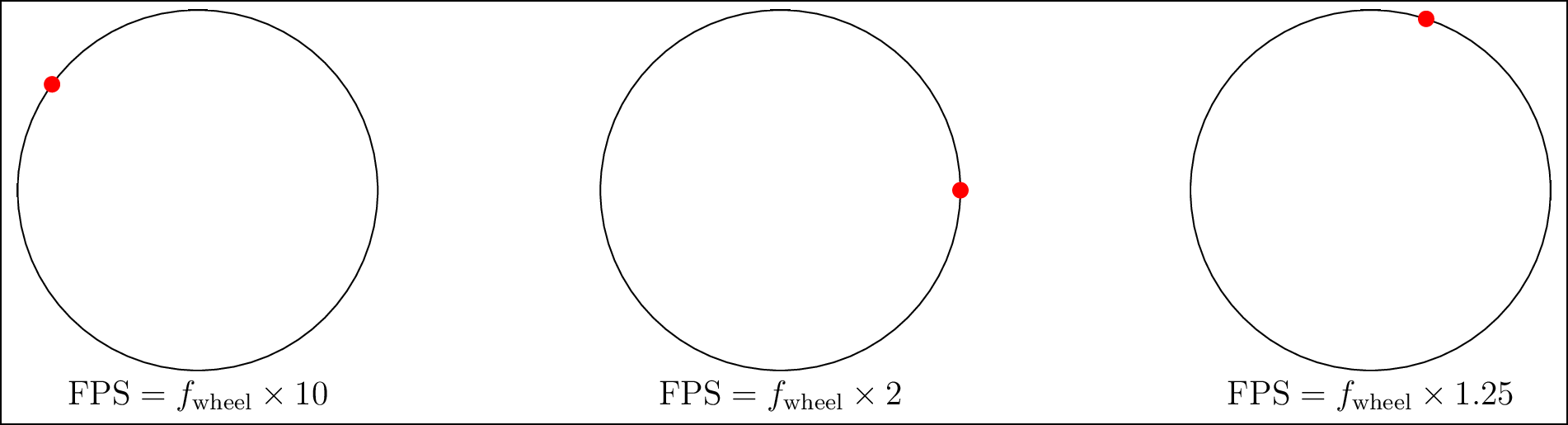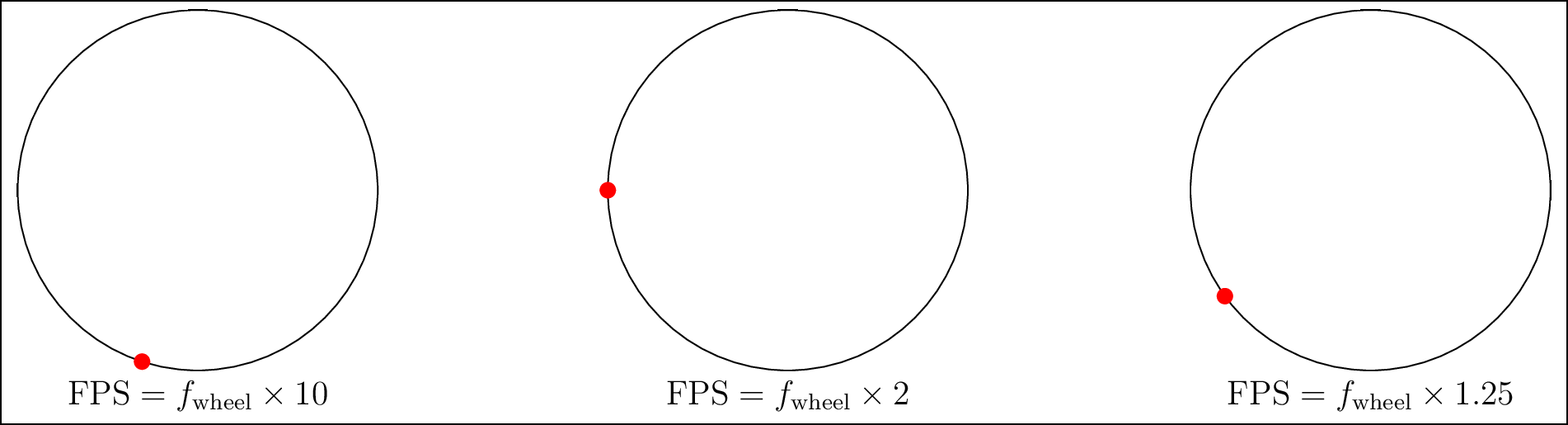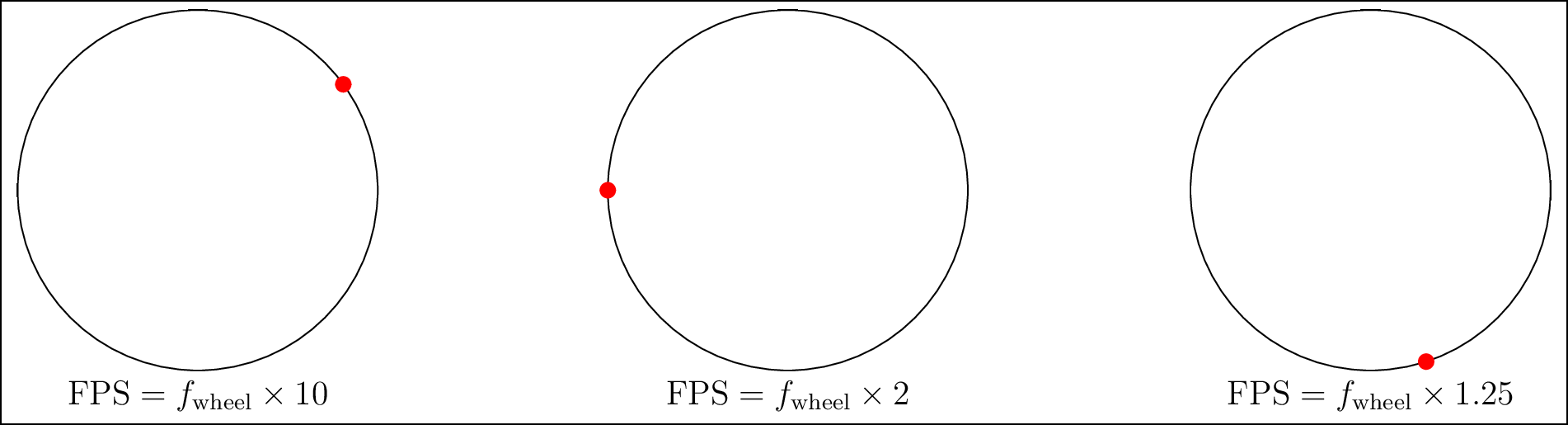
Figure 3.4: The wheen moves clockwise. If the frame rate \(f\) is not more than twice the sampling rate, the rotation of the clockwise moving wheel is incorrectly captured.(see web version for animation).

Some more demonstrations of the wagon wheel effect are given below (see website for the video links).

Can you now comment on the relationship between frequency and samping rate on the faithful representation of the original signal?

The Nyquist criterion

The wagon wheel effect tells us something interesting. It is providing us the condition on the minimum sampling rate required to faithfully reproduce a frequency is strictly more than twice that frequency. If we now extend this concept to any band limited signals, then we realize that band-limited signals are just combinations of various sinusoids (which are analogous to rotating wheels). Thus, to faithfully reproduce a band limited signal, it is clear that the minimum sampling frequency should be more than twice the maximum frequency present in the signal.

Now, if we consider a signal that is band-limited, say possessing frequencies within \([-W, W]\), then that signal can be sampled to obtain a discrete-time signal. If the sampling rate \(f_s\) satisfies \(f_s > 2W\), then it is guaranteed that the signal can be reconstructed with 100% accuracy without any loss of quality. How is this the case?

As an example, consider the signal in Figure 3.5. The baseband bandwidth of the signal is \(W\) Hz, which means that the Fourier transform is non-zero only between \(-W\) and \(W\). If we use the fact that sampling a signal in the time-domain translates to convolution with an impulse train in the frequency domain, we see that if \(T = 1/f_s\) is chosen such that the copies separate without "mixing" with each other. This implies that all information in the signal is captured losslessly, and the original continuous-time signal can be reproduced without error. However, if \(f_s = 1/T \leq 2W\), then we can clearly observe aliasing occurring (marked in red).

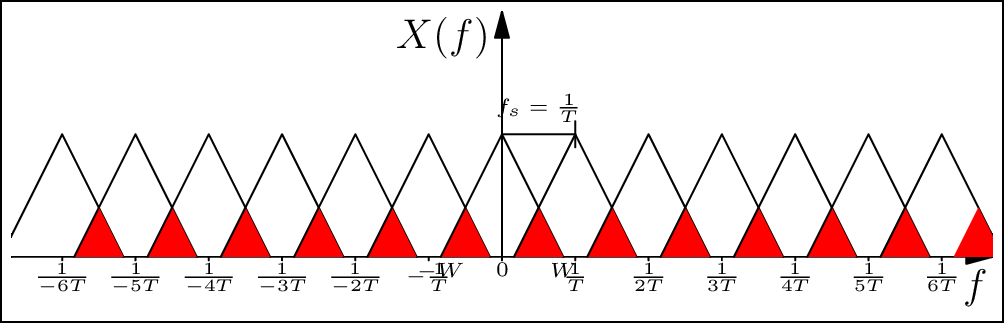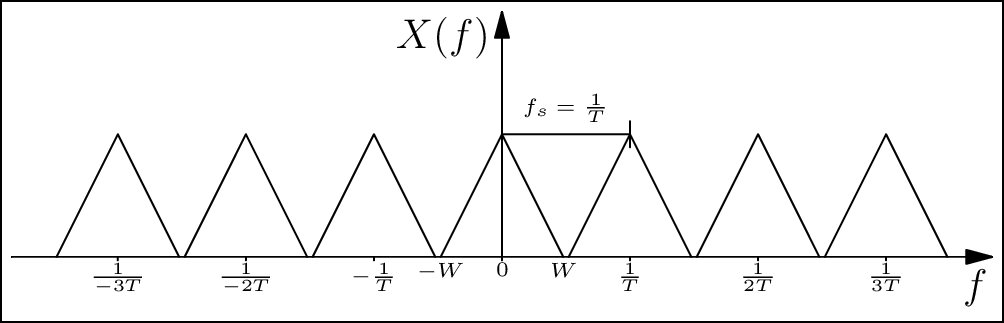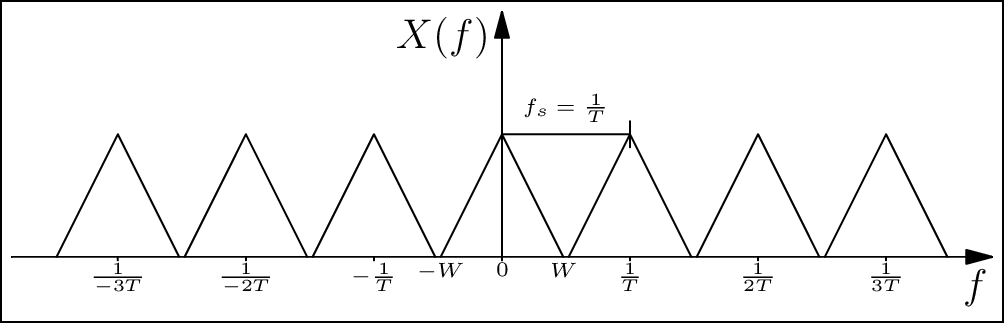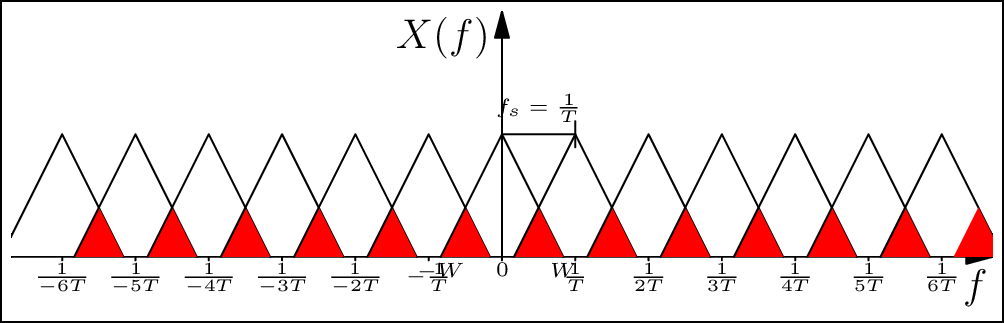
Figure 3.5: If the sampling frequency is not sufficient, aliasing occurs, and this can lead to errors in the digital representation of the signal (see web version for animation).

An important question that arises is this: if sampling works only for band-limited signals, and most real signals are not band-limited, is this even useful? This is a valid consideration, but it can be addressed by viewing this as an engineering problem. As an example, if we consider the \(\mbox{rect}(t)\), its Fourier transform is \(\mbox{sinc}(f)\), whose support is \(f \in (-\infty, \infty)\). However, \(\mbox{sinc}(f)\) decays as \(\frac{1}{f}\), which means that, for large enough \(f\), the values become insignificant. So, if we sample using a large enough \(f_s\), the value of \(\mbox{sinc}(f)\) can be ignored for \(f > f_s\), thus making it practical. In the true mathematical sense, there is a loss in information, but in practice, it may be good enough. Naturally, what is good enough depends on the application, and we will see examples of this during the applications phase of the course.

Figure 3.6: Preventing aliasing using low-pass filtering (see web version for animation).

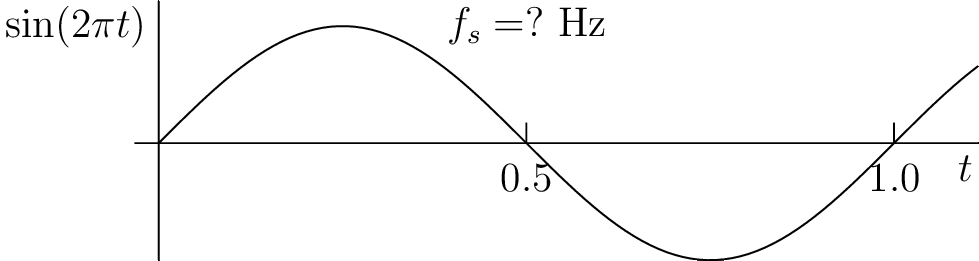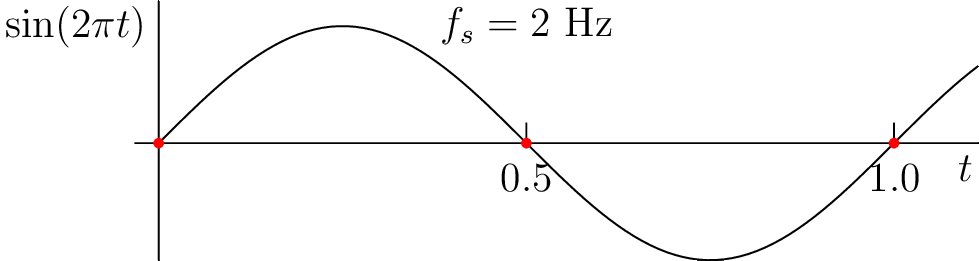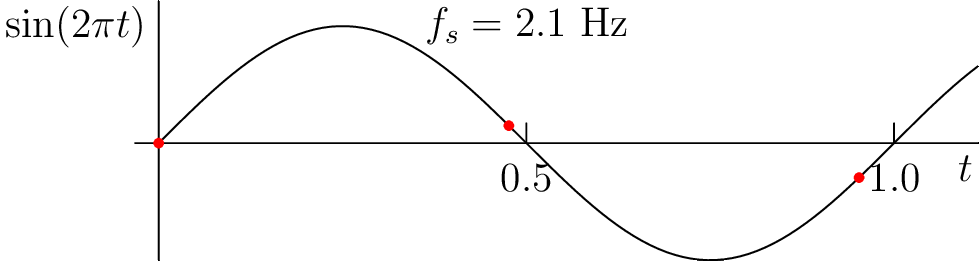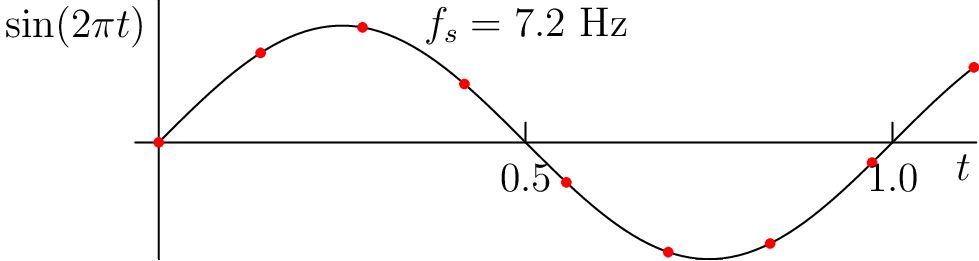
Figure 3.7: Demonstration of aliasing while sampling a 1 Hz sinusoid. (see web version for animation).

Reconstruction of the continuous-time signal

When we are looking at the problem of reconstructing a continuous-time signal, there are now multiple approaches to consider. Remember, the samples that we obtained correspond to a continuous-time signal, and we assume that the samples are spaced \(T = 1/f_s\) seconds apart. We can try any of the following:

• Sample and hold: In this approach, the value of the signal is held constant for the duration of the sample, that is, \(T\) seconds. This is a zeroth order approximation, since we are just assuming that the signal remains constant during each interval of \(T\) seconds. The primary issue with this approach is that there are abrupt jumps after every \(T\) seconds. This is not likely a property that natural signals would satisfy. From a mathematical standpoint, this corresponds to convolving the signal with \(\mbox{rect}(t/T)\).

Figure 3.8: The sample and hold approach to obtain a continuous-time signal from a discrete-time signal.

• Linear interpolation: Another approach which we can try is to linearly interpolate signals. This looks better than the sample and hold approach, but you can still see abrupt changes in the slope. This is also not something you would expect from natural signals. However, both the sample and hold as well as the linear interpolation approaches would work quite well if the sampling rate for the signal is much higher than the bandwidth. Can you figure out why?

Figure 3.9: Although linear intrpolation is better than the sample and hold, we still see sharp transitions and abrupt changes in slope.

• Sinc interpolation: The sinc function is the right function that performs interpolation. This can be seen easily in the frequency domain, since we just need to keep the main "copy" of the repeated copies of the CTFT that appear upon sampling. In the time domain, this translates to an interesting observation: the sinc is a signal that goes to zero at every integer except \(0\). Therefore, if you reconstruct your discrete-time signal as:

\[\begin{equation} x_c(t) \sum_{k = -\infty}^\infty x[n]\text{sinc}\left(\frac{t - kT}{T}\right), \end{equation}\]

then we can see that, whenever \(t = kT\), the value is exactly \(x_c(kT) = x[k]\), and in between there is a combination of the sincs. This can be observed more clearly from the following figures:

Figure 3.10: Observe that the black sinc and red sinc have identical zeros at all points, except, of course, their own peaks.

By combining (adding) the sincs, the zeros at the integer multiples of \(T\) ensures that the precise value of the discrete-time signal is never altered. For instance, even if \(x[1]\) is altered, the constraint that \(x_c(0) = x[0]\) is never changes, as can be seen here:

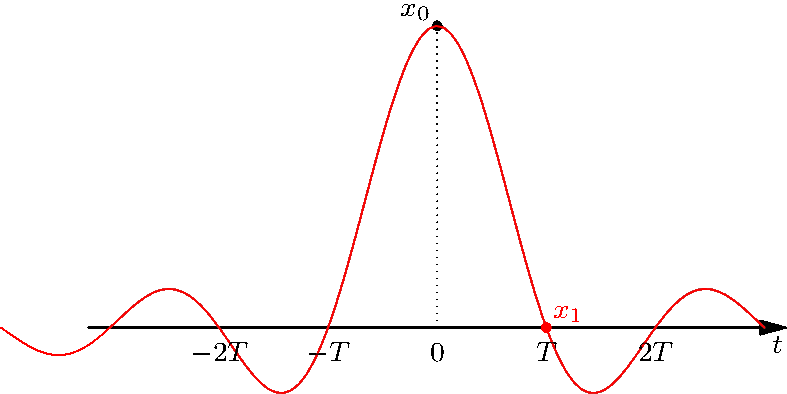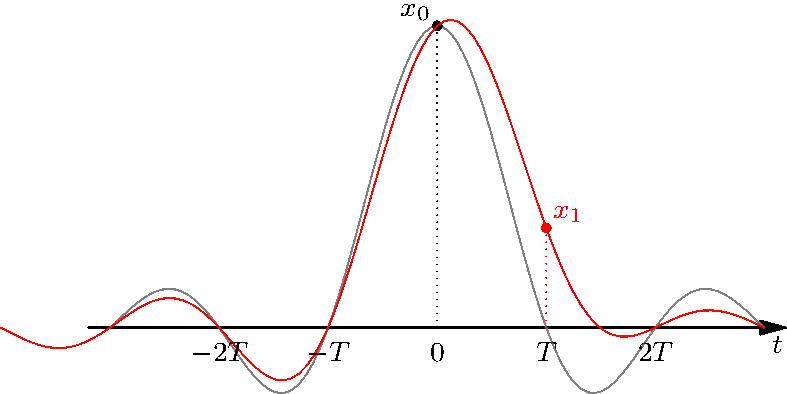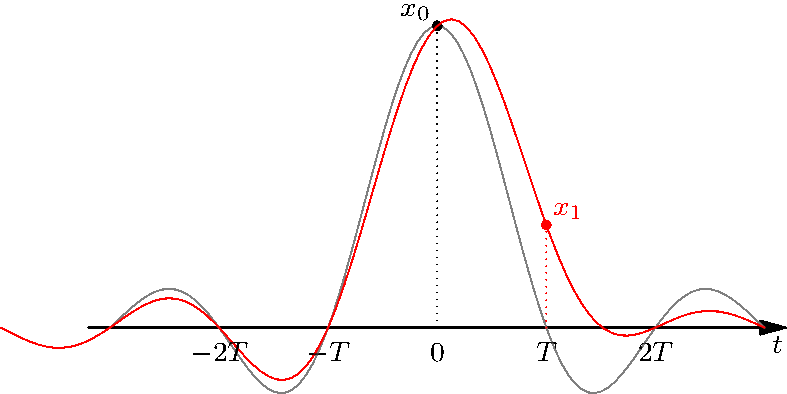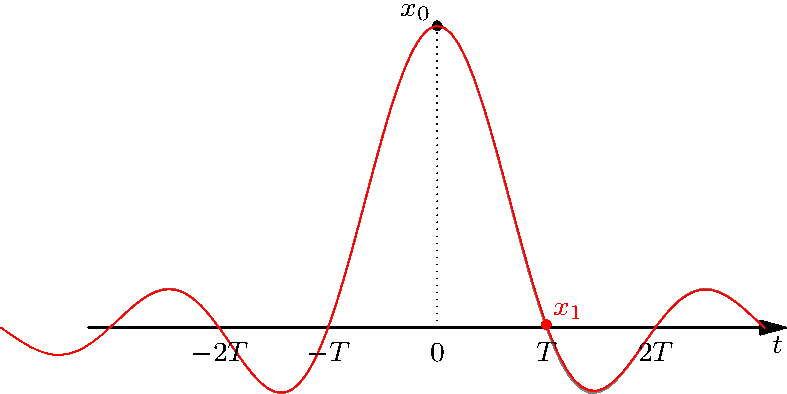
Figure 3.11: Even if we modify some samples, the other values remain unchanged.

One final note is that when we reconstruct CT signals from DT signals, always remember that the original signal was obtained using the band-limited assumption. Given that the original signal was band-limited, the reconstructed signal also has to be band-limited. Thus, even if you consider the discrete-time rectangular window, if you reconstruct the signal, you will find that it does not look like a sharp rectangular window in continuous-time (which is NOT a band-limited signal).

                              The following video has some additional details.  <div style="text-align:center"><iframe width="480" height="270" src="https://www.youtube.com/embed/p9i_boU2tUw?rel=0" frameborder="0" allowfullscreen></iframe></div>  ### More reading material  Definitely watch the [Digital Show & Tell](https://xiph.org/video/vid2.shtml "Digital show & tell") on sampling and quantization. Focus on the sampling part, and understand how sampling works. Please also glance at Chapter 4 of [@oppenheim2001discrete].  <!--chapter:end:02-ct-dt.Rmd-->  # Discrete-time systems {#systems}  In previous chapters, we have explored a little about discrete-time signals and one way to draw a connection between these and continuous-time signals. Largely, our goal was to establish the utility of studying discete-time signals from the perspective of real world applications. In this chapter, we will focus on _systems_, and specifically, _linear time-invariant_ (LTI) systems, owing to their special properties. Since some of these topics are expected to be covered in prior courses, we will just have a simple revision using a video, followed by a focus on LTI systems.  A _system_ is one that takes one or more signals as an input, and produces one or more signals as an output. Such transformations are part and parcel of DSP, since processing signals to remove noise, enhance it, or draw inferences from it is the basic aim of our DSP study. The number of possible transformations of signals is unlimited. However, for the particular case of LTI systems, the output for all inputs can be succinctly described because we can describe the system using a unique signal, called the _impulse response_. This is something that is a natural property of LTI systems that we will exploit significantly.  <div style="text-align:center"><iframe width="480" height="270" src="https://www.youtube.com/embed/4IY6iun2p8c?rel=0" frameborder="0" allowfullscreen></iframe></div>   ## LTI systems  As you have seen, LTI systems have the distinct property that the complete description of the LTI system can be obtained using just the impulse response. This is very convenient, since the system properties can directly be expressed using a signal, and this allows us to characterize the output for every possible input. In particular, as you have seen in the video above, if you know the output for the input $\delta[n]$, which is referred to as the impulse response $h[n]$, then the output for _any_ input can be inferred using superpositions this is the key understanding that we should have about LTI systems.  The other aspect of LTI systems is on how we can practically implement them. In other words, the abstract notion of having an input/output relationship is clear, but how does this translate to an implementation? Let us look at this using some examples. In all of the scenarios below, assume that we get input samples in arrays (typically labeled `x`), and the ouput samples are also stored in arrays (typically labeled `y`). Our starting point for this would be the convolution relationship  \begin{equation} y[n] = \sum_{k = -\infty}^\infty h[k]x[n - k] = \sum_{k = -\infty}^\infty x[k]h[n - k] \end{equation}  We first begin with the two sample average, i.e. $h[n] = 0.5(x[n] + x[n - 1])$. In this case, the convolution operation yields:  \begin{equation} y[n] = (x[n] + x[n - 1]) * 0.5 \end{equation}  If we were to come up with a _realization_ of this system, the question is, what _operations_ would allow you to take the array `x` and give you an array `y`? Here is one example:    So, we now have a for loop that can actually perform the operation that corresponds to this system (Pythonistas may frown at the above solution and come up with a better solution, but this is a start).  Let us now consider a different system. Let us suppose that this LTI system has impulse response $h[n] = (0.9)^n u[n]$. Writing the convolution equation, we get:  \begin{equation} y[n] = \sum_{k=-\infty}^\infty (0.9)^ku[k]x[n - k] = \sum_{k = 0}^\infty x[n - k] \end{equation}  Note that the above is an infinite summation. This makes it difficult to realize, since we cannot implement it in a practical way using loops. However, things can get simplified if we can define a _start_ point for $x[n]$. For example, let us assume that $x[n]$ is zero for $n < 0$. Then, the convolution summation becomes:  \begin{equation} y[n] = \sum_{k=0}^n (0.9)^ku[k]x[n - k] \end{equation}  However, the above form is still not very convenient for implementing directly. But one can realize that there is a recursive formulation for this that can permit an easier realization. That is:  \begin{align} y[0] &= x[0]\\ y[1] &= x[1] + 0.9x[0]\\ y[2] &= x[2] + 0.9x[1] + (0.9)^2 x[0]\\ \vdots &= \vdots \\ y[n] &= x[n] + 0.9x[n - 1] + (0.9)^2x[n - 2] + \cdots + (0.9)^{n-1}x[0]\\ \end{align}  If you look carefully, the last equation above points to a _recursive_ implementation. That is, you can express $y[n]$ as $x[n] + 0.9y[n - 1]$. This is the so-called recursive realization of IIR filters.  In general, one can express the realization of LTI systems in terms of simple equations that relate the input $x[n]$ with the output $y[n]$. These are called linear constant coefficient difference equations (LCCDEs). More generally, it consists of linear combinations of $x[\cdot]$ and $y[\cdot]$.  The concept of _causality_ is one that appears frequently. A causal system is one whose output depends only on current and past inputs. This matters for real-time implementations, since the current outputs can only be a function of the inputs that you already have or those that came in the past. However, for contexts that involve offline processing, or something like images, where the concept of _time_ doesn't make sense, causality is not a necessity. Mathematically, for LTI systems, causality implies that the impulse response satisfies $h[n] = 0$ for $n < 0$.  ## Stability of LTI systems  In the context of DSP, stability is an important concept that is connected with the design and analysis of systems. In particular, the concept of _stability_ refers to whether the _output_ of a system is guaranteed to be bounded if the input is bounded. Why is this important?  One practical constraint in many DSP implementations is that these are typically implemented using finite precision systems. Therefore, if we are not careful with regard to the design of LTI systems, finite inputs can cause the outputs to become large, and go out of bounds. As an example, if we are focusing on a noise reduction system, if the system actually amplifies inputs and the corresponding outputs cannot be represented without any distortion. One way to prevent this from happening is to ensure that our systems satisfy the _bounded-input bounded-output_ (BIBO) condition. That is, whenever the input $x[n]$ satisfies $|x[n]| < M_x$ for a positive real number $M_x$, then the output $y[n]$ satisfies $|y[n]| < M_y$ for a positive real number $M_y$. One key way to check this for LTI systems is to just evaluate the absolute sum of the impulse response. If this absolute sum is finite, then the system is stable, and vice-versa. How? Let us first verify that if the system is indeed stable, then the absolute sum of $h[n]$ is finite. For this, choose the input $x[n]$ as $\text{sgn}(h[-n])$. That is, $x[n] = 1$ if $h[n] > 0$, and $x[n] = -1$ when $h[n] < 0$. Then, we have:  \begin{align} y[0] &= \sum_{k = -\infty}^\infty x[k]h[k] \\ &= \sum_{k = -\infty}^\infty x[k]\text{sgn}(h[k]) \\ &= \sum_{k = -\infty}^\infty |x[k]| < M_y \end{align}  Thus, it is clear that stablity translates to absolute summability for LTI systems. But does the converse hold true? That is, if the impulse response of the LTI system is absolutely summable, then can you conclude that the system is stable?  For this situation, let us assume that the impulse response LTI system $|h[n]|$ is absolutely summable, but that the system is not stable. Then, there must exist a bounded input $x[n]$ with $|x[n]| < M_x$ such that the output $y[n]$ is unbounded. Therefore, $\sum_k x[k]h[n - k]$ is unbounded. However, this is not possible, since $\sum_k |x[k]||h[k]| \leq M\sum_k|h[k]|$, which is finite due to the absolute summability of $h[k]$. This leads to a contradiction. Thus, absolute summability and stability have an if-and-only-if relationship.   <div style="text-align:center"><iframe width="480" height="270" src="https://www.youtube.com/embed/9SduliJJp-g?rel=0" frameborder="0" allowfullscreen></iframe></div>  ## Complex exponentials are eigenfunctions of LTI systems  Another important property of LTI systems is the fact that, if the input to these systems is the complex exponential, the output is just a _scaled_ version of the same complex exponential. That is, if the input $e^{j\omega_0 n}$ is given to the system whose impulse response is $h[n]$, we have  \begin{equation} y[n] = \sum_{k = -\infty}^\infty h[k] e^{j\omega_0 (n - k)} = e^{j\omega_0 n}\sum_{k = -\infty}^\infty h[k] e^{-j\omega_0 k}. \end{equation}  In other words, the output is just a scaled version of the same complex exponential. This provides a natural concept of the relationship between frequency and LTI systems: LTI systems only _scale_ existing frequency components. They do not add new frequencies. This also provides you a hint on what _filters_ are. For example, in the context of audio equalizers (where you can change the bass, treble etc.), scaling various frequencies up and down is something that can be done using filters. Another example that is common is for correcting channel effects across frequencies in communication systems. This will become more clear as we discuss the discrete-time fourier transform (DTFT) in the next chapter.  <!--chapter:end:03-signals-and-systems.Rmd-->  # The Discrete-time Fourier Transform and $z$-transform {#transforms}  Transform based analysis of discrete-time signals and systems is an essential part of DSP, primarily because it provides an essential alternate view of the properties of signals and systems. These transforms enable us to not only spot interesting properties of these signals, but also predict their behaviour when different signals and systems interact with each other. This chapter will focus on LTI systems and their transform analysis using the DTFT and $z$-transforms.  ## The discrete-time Fourier transform  As we have seen in the previous chapter, the complex exponential is an eigenfunction of LTI systems. That is, if the input \( e^{j\omega_0 n} \) is given to an LTI system, the output is just a scaled version of the same. In fact, thie output is the DTFT. To establish the existence of a finite value of the DTFT, the output would have to be well defined for every value of \( \omega_0 \in [-\pi, \pi) \). To establish a condition for this, notice that the signal \( e^{j\omega_0 n} \) is a signal that is bounded (its absolute value is always $1$). Therefore, whenever it is convolved with a stable LTI system, the output will always be bounded. What is the implication? The output of a stable system is always bounded when the input is a complex exponential. In other words, if a signal \( h[n] \) is _absolutely summable_, that is a sufficient condition for us to define the DTFT. Thus, for absolutely summable signals, we have  \begin{equation} H(e^{j\omega}) = \sum_{n = -\infty}^\infty h[n]e^{-j\omega n} \end{equation}  Note that absolute summability is only a sufficient but not necessary condition. So, the DTFT can be defined for some signals that are not absolutely summable as well, such as \( \cos \omega_0 n \), \( u[n] \) etc., although they generally involve the use of impulses.  One important property to note is that the DTFT is periodic, and has period \(2 \pi \). This has a direct connection with the sampling theorem, as explained in this video:  <div style="text-align:center"><iframe width="480" height="270" src="https://www.youtube.com/embed/ULJ_nvhQPE8?rel=0" frameborder="0" allowfullscreen></iframe></div>   ### The notion of frequency  One aspect that is interesting in digital signals is that the notion of frequency is different from that in continuous-time. The frequency \( \omega \) is a number between \( -\pi \) and \( \pi \). The reason for this becomes clear by understanding the frequency as a concept of variation of consecutive values.   ```python import plot_helper import pylab as p N = 5 n = p.r_[-N:N+1] x = (-1.0)**n plot_helper.stemplot(n, x, title=r'$x[n] = (-1)^n$', filename='minus_one_p_n.svg')            

Figure 3.12: The alternating sequence.

If we observe the \((-1)^n\) sequence, we see that it is a periodic sequence whose value alternates for every value of \(n\). Any other sequence would not have a faster rate of variation. In fact, you can observe this easily by seeing that \((-1)^n = e^{j\pi n}\). Similarly, the all ones sequence is the periodic sequence that has zero frequency, as \(e^{j 0 n} = 1\).

An intuition on why this holds can be understood by thinking about it in terms of sampling. If we sample a signal at \(f_s\) samples per second, Nyquist sampling theorem indicates that the range of frequencies that can be represented in the digital domain is limited to be between \([-f_s / 2, f_s / 2]\). Thus, observing it pictorially, the way you did in the case of sampling, would make things clear.

Properties of the DTFT

The properties of the Discrete-time Fourier transform can be seen from (Oppenheim, Buck, and Schafer 2001), but the key properties are summarized in the video below.

One key property is the convolution property, that basically implies that the DTFT of the convolution of two time-domain sequences is the product of the respective signals' DTFTs. This is something that would come in very handy when solving problems and gaining intuitions on system properties.

The \(z\)-transform

Much like the Laplace transform in continuous-time systems, the \(z\) transform is a generalization of the DTFT, and is able to capture the property of a larger class of signals. Take, for example, \(2^n u[n]\), or even \(u[n]\), for that matter. These signals do not have DTFTs. However, the \(z\)-transform exists for these signals. The definition is:

\[\begin{equation} X(z) = \sum_{n = -\infty}^\infty x[n] z^{-n}, |z| \in \text{ROC} \end{equation}\]

The importance of the ROC becomes evident with a simple example. Consider the sequence \(x_1[n] = a^n u[n]\). Substituting in the above formula, we get the following:

\[\begin{equation} X_1(z) = 1 + az^{-1} + a^2z^{-2} + a^3z^{-3} + \ldots \end{equation}\]

The above summation converges only when \(|az^{-1}| < 1\). That is, the ROC is \(|z| > |a|\). Then, we get

\[\begin{equation} X_1(z) = \frac{1}{1 - az^{-1}}, |z| > |a| \end{equation}\]

Now, if we repeat the above exercise for \(x_2[n] -a^n u[-n - 1]\), we get

\[\begin{equation} X_2(z) = -a^{-1}z - a^{-2}z^2 - a^{-3}z^3 - \ldots \end{equation}\]

The above summation converges only for \(|a^{-1}z| < 1\), that is, the ROC is \(|z| < |a|\), and simplifying yields

\[\begin{equation} X_2(z) = \frac{1}{1 - az^{-1}}, |z| < |a| \end{equation}\]

It is clear that the right-sided sequence \(x_1[n]\) and the left-sided sequence \(x_2[n]\) have the same expression as their \(z\)-transform. However, the ROC establishes the precise sequence that they correspond to. Therefore, in general, the \(z\)-transform is unspecified if the ROC is not specified.

Properties of the ROC

The ROC has some distinctive properties that are useful to keep in mind when dealing with \(z\)-transforms. In particular, remember the following:

1. The ROC is always of the form \(0 \leq r_R < |z| < r_L \leq \infty\), where \(r_R, r_L\) are positive real numbers, and \(r_L\) can also be \(\infty\).

2. Left-sided sequences have ROCs of the form \(|z| < |a|\).

3. Right-sided sequences have ROCs of the form \(|z| > |a|\).

4. The ROCs are always contiguous regions and never interesections of disjoint regions.

Inverting \(z\)-transforms

In genereal, inverting \(z\)-transforms requires integration over contours, and we will not be covering this approach in our course. Instead, we will consider the following approaches:

1. By inspection: Since many common \(z\)-transforms have common forms, we can directly invert them by inspection. For example, if you are given the \(z\)-transform \(1 / (1 - 0.5z^{-1}\) and \(|z| > |a|\), then we can directly use the general form to write the inverse as \((0.5)^n u[n]\).

2. Partial fractions: When we have forms like \(1 / (1 - az^{-1})(1 - bz^{-1})\), one can do a partial fraction expansion to get it to a simpler form, and then we can invert it by inspection.

3. Power series expansion: For sequences that admit a power series expansion, the power series can directly provide the sequence inverse. For example:

\[\begin{equation} X(z) = \log (1 + az^{-1}) = az^{-1} - \frac{a^2z^{-2}}{2} + \frac{a^3z^{-3}}{3} + \ldots = \sum_{n = 1}^\infty \frac{(-1)^{n+1}}{n}z^{-n} \end{equation}\]

Properties of \(z\)-transforms

The common properties of \(z\)-transforms are similar to that of DTFTs, with some subtle differences. These can be summarized as:

1. Linearity: If the \(z\)-transform of \(x[n]\) and \(y[n]\) are, respectively \(X(z)\) and \(Y(z)\), then the \(z\)-transform of \(\alpha x[n] + \beta y[n]\) for any two complex numbers is \(\alpha X(z) + \beta Y(z)\). This can directly be observed from the linearity property in the \(z\)-transform summation. The ROC is at least the intersections of the ROCs of \(X(z)\) and \(Y(z)\).

2. Time shifting: Since the \(z\)-transform of \(\delta[n - n_0]\) is \(z^{-n_0}\) for every integer value, if the \(z\)-transform of \(x[n]\) is \(X(z)\), then the \(z\)-transform of \(x[n - n_0]\) is \(z^{-n_0} X(z)\). The ROC remains unchanged.

3. Exponential multiplication: Multiplying a sequence \(x[n]\) with a complex exponential, such as \(z_0^n\), would result in the \(z\)-transform being converted to the new \(z\)-transform \(X(z / z_0)\), and the ROC is scaled by a factor of \(|z_0|\).

4. Differentiation: If we differentiate the \(z\)-transform and multiply by \(-z\), then we get the \(z\)-transform of the sequence that is multiplied by \(n\). That is, if \(x[n]\) has a \(z\)-transform of \(X(z)\), then \(nx[n]\) would have a \(z\)-transform of \(-z dX(z) / dz\). The ROC is at least the ROC of the original \(z\)-transform.

5. Conjugation: If \(X(z)\) is the \(z\)-transform of \(x[n]\), then \(x^*[n]\) has \(z\)-transform \(X^*( z^* )\), with the same ROC.

6. Time reversal: If \(x[n]\) has \(z\)-transform \(X(z)\), then \(x[-n]\) has \(z\)-transform \(X(1/z)\), with the ROC taking the reciprocal values of the original ROCs.

7. Convolution: As discussed earlier, if \(x[n]\) and \(y[n]\) have \(z\)-transforms \(X(z)\) and \(Y(z)\) respectively, then the sequence \(x[n] * y[n]\) has \(z\)-transform \(X(z)Y(z)\), with the ROC being at least the intersection of the ROCs of the original sequences.

Some common examples and connection with DTFTs

Application of DTFT: Ideal low-pass filters and fractional delays

To gain some more insights into DTFTs, we will now look at two examples. The first one we will consider is the ideal low-pass filter. The ideal low-pass filter with a cut-off frequency of \(\omega_c\) can be defined as the periodic extension of

\[ H(e^{j\omega}) = \begin{cases} 1 &\mbox{if } |\omega| < \omega_c \\ 0 & \mbox{if } \omega_c \leq |\omega| < \pi \\ \end{cases} \]

Always remember that there is a \(2\pi\) periodic extension of the above sequence. If you use the inverse DTFT formula, we end up with the sequence

\[ h[n] = \frac{\sin \omega_c n}{\pi n} \]

Notice that, for \(n = 0\), the value is defined to be \(h[0] = \omega_c / \pi\). Notice that this is an infinite length sequence, and realizing this filter as an LCCDE is not possible. Given that this is the case, the ideal LPF is not practically realizable. Having said that, we will still try to analyze this system. Here is one way:

                                                      import                    numpy                    as                    np                                      import                    pylab                                      from                    scipy.signal                    import                    freqz                                    omega_c                    =                    np.pi                    /                    2                                    N                    =                    100                                    n                    =                    np.arange(-N, N                    +                    1)                  h                    =                    omega_c                    /                    np.pi                    *                    np.sinc(omega_c                    *                    n                    /np.pi)                  [W, H]                    =                    freqz(h, worN=                    4096)                                    pylab.rc('text', usetex=                    True)                  pylab.rc('font', size=                    16)                  pylab.rc('axes', labelsize=                    16)                  pylab.rc('legend', fontsize=                    12)                  pylab.plot(W,                    20                    *np.log10(np.abs(H)))                  pylab.grid(True)                  pylab.xlabel(r'$\omega$')                  pylab.ylabel('$|H(e^{j\omega})|$ (dB)')                  pylab.axis([0, np.pi,                    -                    50,                    3])                              

                                  pylab.savefig('lpf1.svg')                              

Figure 3.13: The magnitude response of a truncated LPF.

Notice in the above that there is a significant ripple. This ripple can be attributed to the truncation of the ideal LPF. This operation, called windowing, causes a convolution of the ideal LPF DTFT with that of the window. The following video describes this in detail:

A similar, and useful, application, is that of the fractional delay. Consider the DTFT \(H(e^{j\omega}) = e^{-j\omega \alpha}\), where \(\alpha\) is a real number. In this case, if \(\alpha\) is an integer, then the sequence that this DTFT corresponds to is \(\delta[n - \alpha]\). However, this becomes interesting when \(\alpha\) is not an integer. In this case, using the DTFT formula yields:

\[ h[n] = \frac{\sin(\pi (n - \alpha))}{\pi(n - \alpha)}. \]

The above sequence can easily be recognized as a sinc that is sampled at non-integer points. What is interesting is that, by not sampling exactly at integer locations, ALL the sinc points start coming into the picture. This looks puzzling initially, but will become clear if you observe the following video:

If you view the discrete-time signal \(\delta[n]\) as just being reconstructed to a sinc, then convolving with the sequence that corresponds to \(H(e^{j\omega}) = e^{-j\omega \alpha}\) results in resampling the sinc at different points. More here:

Group delay and linear phase

The concept of group delay helps understand the amount of delay that the envelope of a signal is subjected to. This would become clear using an example.

                                                      import                    numpy                    as                    np                                      import                    pylab                                      from                    scipy.signal                    import                    freqz                                    n                    =                    np.arange(-                    20,                    21)                  g                    =                    np.exp(-n**                    2                    /                    400)                                    M                    =                    30                                    h                    =                    np.ones(M)                    /                    M                  y                    =                    np.convolve(h, g)                                    pylab.figure()                  pylab.rc('text', usetex=                    True)                  pylab.rc('font', size=                    16)                  pylab.rc('axes', labelsize=                    16)                  pylab.rc('legend', fontsize=                    12)                  pylab.plot(n, g,                    'r-', label=                    r'$x[n]$')                  n                    =                    np.arange(-                    20,                    21                    +                    M                    -                    1)                  pylab.plot(n, y,                    'b-', label=                    r'$y[n]$')                  pylab.grid(True)                  pylab.xlabel(r'$n$')                  pylab.ylabel('$x[n], y[n]$')                  pylab.legend()                  pylab.savefig('gaussian1.svg')                              

Figure 3.14: Filtering the signal using the 30-length rectangular pulse delays the resulting sequence precisely by 15 points.

In the above example, a Gaussian pulse is filtered using a 30 length rectangular window. We observe that that resulting pulse has its peak delayed by around 15 units (14.5 to be precise). Why is this the case? This can be understood using the group delay definition. We can define the group delay of the filter \(h[n]\), whose DTFT is \(H(e^{j\omega})\) as \(\frac{d\angle H(e^{j\omega})}{d\omega}\). For the 30 length rectangular window, you can find that this works out to \(14.5\). You can clearly see that the signal gets delayed and slightly modified, but looks largely undistorted.

In general, the group delay depends on the frequency \(\omega\), which is why different components of signals can get delayed by different amounts. As an example, consider \(h[n] = \delta[n] + 0.5\delta[n - 1]\). In this case, \(\angle H(e^{j\omega})\) works out to \(\tan^{-1} \frac{0.5\sin \omega}{1 + 0.5\cos \omega}\). In this case, the group delay changes with \(\omega\). This can be seen from the plot below.

                                                      import                    numpy                    as                    np                                      import                    pylab                                      from                    scipy.signal                    import                    freqz                                    n                    =                    np.arange(-                    20,                    21)                  g                    =                    np.exp(-n**                    2                    /                    400)                                    M                    =                    30                                    h                    =                    np.ones(M)                    /                    M                  h[M//                    2:]                    =                    h[M//                    2:]                    /                    2                                    y                    =                    np.convolve(h, g)                                    pylab.figure()                  pylab.rc('text', usetex=                    True)                  pylab.rc('font', size=                    16)                  pylab.rc('axes', labelsize=                    16)                  pylab.rc('legend', fontsize=                    12)                  pylab.plot(n, g,                    'r-', label=                    r'$x[n]$')                  n                    =                    np.arange(-                    20,                    21                    +                    M                    -                    1)                  pylab.plot(n, y,                    'b-', label=                    r'$y[n]$')                  pylab.grid(True)                  pylab.xlabel(r'$n$')                  pylab.ylabel('$x[n], y[n]$')                  pylab.legend()                  pylab.savefig('gaussian2.svg')                              

Figure 3.15: Filtering the signal using a different pulse causes the resulting sequence to exhibit some distortion.

Thus, in general, the non-linearity of the group delay causes distortion of the signal, since different frequencies are delayed by different amounts, and the modifications are not as you would ideally expect, as in the case of just the magnitude response.

However, there are certain constraints that can be imposed on the impulse response of the filter to obtain a constant group delay, thereby minimizing the undesired distortion. They are specified by the following types:

1. Type-1 linear phase FIR filter: A filter is said to be a Type-1 FIR filter if its impulse response is defined for \(n = 0, 1, 2, \ldots M\), where \(M\) is an even number, and \(h[n] = h[M - n]\). This ensures that the filter has constant group delay. This can be proved very easily:

   \[\begin{equation} H(e^{j\omega}) = h[0] + h[1]e^{-j\omega} + h[2]e^{-j2\omega} \ldots h[M]e^{-jM\omega} \end{equation}\]

   The above can be simplified easily to:

   \[\begin{equation} H(e^{j\omega}) = e^{j\omega M /2}(2h[0] \cos (M \omega / 2) + 2h[1] \cos ((M - 1) \omega / 2) + \ldots + h[M/2]) \end{equation}\]

   It can be seen very clearly that the group delay of the filter for all \(\omega\) is \((M - 1) / 2\), since the part in the bracket is real, and thus, contributes only a phase of \(0\) or \(\pi\), depending on the sign. This is a useful constraint that we will look at again in the context of filter design.

2. Type-2 linear phase FIR filter: A filter is said to be a Type-2 FIR filter if its impulse response is defined for \(n = 0, 1, 2, \ldots M\), where \(M\) is an odd number, and \(h[n] = h[M - n]\). This is similar to the previous one, except that he filter has an even number of coefficients.

3. Type-3 linear phase FIR filter: A filter is said to be a Type-3 FIR filter if its impulse response is defined for \(n = 0, 1, 2, \ldots M\), where \(M\) is an even number, and \(h[n] = -h[M - n]\). This is similar to Type-1, except that the impulse response is anti-symmetric around the middle.

4. Type-4 linear phase FIR filter: A filter is said to be a Type-4 FIR filter if its impulse response is defined for \(n = 0, 1, 2, \ldots M\), where \(M\) is an odd number, and \(h[n] = -h[M - n]\). This is similar to Type-2, except that the impulse response is anti-symmetric around the middle.

One common aspect that you can see in the above is that there is an inherent symmetry, and that is leading to the linear phase condition. In fact, for both Type-1 and Type-3 filters, shifting them to the left would make them symmetric (or anti-symmetric) about zero, thereby leading to the situation that the DTFT is purely real or imaginary, causing the group delay to be \(0\). For the Type-2 and Type-4 filters, a fractional shift to the left would be needed, but there is symmetry there as well. This can be verified by writing out the DTFT and verifying it for yourself.

The all-pass minimum-phase decompsition

References

Oppenheim, Alan V, John R Buck, and Ronald W Schafer. 2001. Discrete-Time Signal Processing. Vol. 3. Upper Saddle River, NJ: Prentice Hall.

Oppenheim, Alan V, AS Willsky, and SH Nawab. 2005. "Signals and Systems." Prentice Hall) Pp128.

wardhicies.blogspot.com

Source: https://www.ee.iitb.ac.in/~akumar/courses/ee603-2020/sampling.html

Share this post